Rationale
In today’s world, exceptional computational skills in mathematics, though highly desirable, are not enough. Students need the ability to think, analyze, synthesize and solve word problems. As a fourth grade teacher, my students operate computationally at a high level. However, they struggle when it comes to problem solving. My strategy is to provide students with new tools to help them become more confident and accomplished solvers of word problems. I plan on introducing my students to a system known as Number Talks.
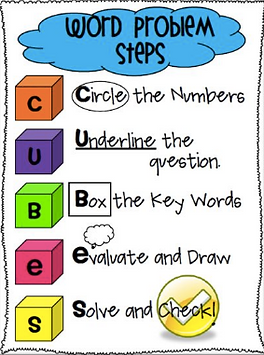
At the beginning of the year, I spoke with the mathematics curriculum facilitator and my CADRE associate and we wanted to focus on an area in which students needed assistance. Thus far, the system I have been employing with my students is based upon the acronym, CUBE. CUBE stands for: circle the numbers, underline important words, box the question and evaluate. Though this system has been valuable it does have drawbacks. My students are computationally driven and often are not flexible in the manner in which they think. If one of the steps in the CUBE process is not extremely transparent, students become frustrated and impatient. They just want to get to the answer. I am hopeful the implementation of Number Talks will help to alleviate students' frustration and improve their ability to analyze, strategize and communicate. This journey will take my students from computation to comprehension.
Number Talks will provide students with a more flexible way to promote problem solving and metacognition. Students will collaborate and communicate their ideas with each other. This will be a new experience for the students. Students need to feel comfortable expressing their thought processes and be willing to take academic risks. In addition, students must be respectful of one another and encouraged to work as a team. This interaction will allow students to listen to how their peers think and analyze a given problem. These engagements will happen in the students' own words and lead to a more collaborative atmosphere. My role will be to facilitate the student interactions, guiding them along the way. In addition, I will be learning how my students think. It will be enlightening for me to observe how students process information as they exchange ideas. I want students to see the connection between their computational skills and problem solving. Ultimately, the classroom should be a place where students construct viable arguments, explain their thoughts and respond to their peers' thinking.
Teaching fourth grade mathematics to a wide array of students has brought me to the realization that, in general, my students possessed good computation skills but lacked the ability to express a deeper understanding of mathematical concepts. I felt there was a need to have students become more engaged in problem solving. The students needed a technique to facilitate and improve their problem solving comprehension. The decision to incorporate Number Talks will serve to accomplish these goals.
All too often, students are only concerned with obtaining an answer through rote calculation. Little thought is given to understanding the context of the problem (Verschaffel, De Corte and Vierstraete, 1999). Number Talks will serve as a tool to get students to verbally communicate with one another and show how they reasoned and arrived at their conclusions. The purpose of discourse is not for students to state their answers and get validation from the teacher but to engage all learners and keep the cognitive demand high (Breyfogle and Williams, 2008-2009). Mathematics educators nationwide agree that student engagement in meaningful mathematical discourse has a positive effect on their mathematical understanding as they increase the connections between ideas and representations (de Garcia, Math Solutions).
In order for Number Talks to be effective, the following components must be addressed. These components are: classroom environment and community, the teacher’s role, the role of mental math and purposeful computation problems (Parrish 2010). In essence, the entire process must be constructed, implemented, facilitated and encouraged by the instructor. Turner et al. (2003) stated four ways in which teachers communicate with students: (1) messages about tasks, learning, and expectations for students; (2) relationships with teacher; (3) relationships among students; and (4) rules and management structures. In the week leading up to the actual implementation of Number Talks, I will be working with students, developing appropriate communication skills in order to lay the foundation for productive class interactions for when we begin working with word problems.
Once students understand the expectations and norms, it will be my job to best facilitate the discourse. The challenge will be to determine how to improve student participation and conceptual understanding. Hufferd-Ackles et al (2004) outline four levels of discourse. Level 0- The teacher introduces mathematical ideas and asks questions. Then, students listen and give short answers. Level 1- The teacher asks students direct questions about their thinking while others listen. The teacher explains student strategies, filling in gaps before continuing to present mathematical ideas. The teacher may ask one student to help another by showing how to do a problem. Level 2- The teacher asks open-ended questions and asks students to comment on one another’s work. Students answer the questions posed to them and voluntarily provide additional information about their thinking. Level 3- The teacher facilitates the discussion by encouraging students to ask questions of one another to clarify ideas. Ideas from the community build on one another as students thoroughly explain their thinking and listen to the explanations of others. It is my hope, that the class will begin our Number Talks at Level 1 and then move on to Level 2 as students gain more confidence in their thinking process.
There are numerous methodologies and techniques teachers can employ to facilitate, encourage and direct classroom discussions. Some of the most productive techniques are provided by Chapin, O’Connor and Anderson (2003). There are five major components on which I will focus: (1) revoicing, (2) asking students to restate someone else’s reasoning, (3) asking students to apply their own reasoning to someone else’s reasoning, (4) prompting students for further participation and (5) using wait time. These techniques are supported by posters which have been provided by John Becker, Curriculum Advisor and CADRE Associate.
The implementation of a process which challenges students to think and reason is grounded in theory and research on how students learn (Smith and Stein, 2011). It is my goal to take my students on a journey from computation to comprehension using a Number Talks design and philosophy.
Research